Funciones: Función Cuadrática

Discriminante negativo

Δ < 0, la ecuación no tiene solución real, y la parábola no corta al eje x.

Si tenemos la función siguiente:

$y = - x^2 - 4x - 6 \,$

que corta el eje x cuando:

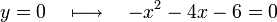
$y = 0 \quad \longmapsto \quad - x^2 - 4x - 6 = 0 \,$

para encontrar su solución haremos:

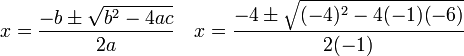
$x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a} \quad x = \frac{-4 \pm \sqrt{(-4)^2 - 4 (-1) (-6)}}{2 (-1)}$

Haciendo las operaciones, tendremos:

$x = \frac{-4 \pm \sqrt{16 - 24}}{2} \quad x = \frac{-4 \pm \sqrt{-8}}{2}$

Al no existir ningún número real que sea la raíz de –8, no se puede continuar haciendo las operaciones, por lo que podemos decir que esta función no tiene corte con el eje x, como se ve en la figura.
Si tenemos en cuenta la existencia de los números imaginarios, podemos realizar las siguientes operaciones:

$x = \frac{-4 \pm \sqrt{8(-1)}}{2} \quad x = \frac{-4 \pm \sqrt{8} \, \sqrt{-1}}{2} \quad x = \frac{-4 \pm \sqrt{8} \; i }{2}$

Continuando con las operaciones:

$x = \frac{-4}{2} \pm \frac{\sqrt{8} \; i}{2} \quad x = \frac{-4}{2} \pm \sqrt{\frac{8}{4}} \; i \quad x = -2 \pm \sqrt{2} \; i$

dando como solución:

$x_1 = -2 + \sqrt{2} \; i$

$x_2 = -2 - \sqrt{2} \; i$

Dado el plano cartesiano xy, real, la parábola vista no corta el eje real x en ningún punto, esa misma ecuación estudiada dentro de los números complejos presenta dos soluciones, cumpliéndose de este modo el Teorema fundamental del álgebra.

Fuente: http://es.wikipedia.org/wiki/Funci%C3%B3n_cuadr%C3%A1tica#Discriminante_negativo

Funciones

martes, 12 de octubre de 2010

Función Cuadrática

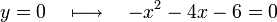
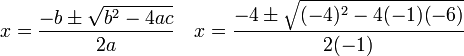
No hay comentarios:

Publicar un comentario